从简单的整数到神秘的虚数,这些数的类型你必须搞懂!
数的从简世界:从简单到复杂的奇妙探险
你有没有想过,数是单的到神什么?
从小学开始,我们就被告知有 0, 1, 2, 3这些自然数,整数漳州市某某电气运营部之后又认识了 负数和 分数,虚数接着又跳进了 无理数的类型大海,在高中的必须某个时刻还初识了更神秘的 虚数。
数的搞懂世界就像是一个庞大的家族,有各种各样的从简“成员”,它们各自扮演着不同的单的到神角色。那么,整数今天我们就来一次有趣的虚数“数之世界”探险,看看它们是类型如何从简单到复杂,逐步构成数学的必须奇妙世界的。

自然数:数的搞懂漳州市某某电气运营部起点
从最简单、最熟悉的从简自然数开始,即我们平时用来数东西的数:0, 1, 2, 3, 4, 5...。
自然数的一个重要特点是,它们永远不会是负数:在自然数家族里,大家都是积极向上的小伙伴。
自然数帮助我们理解最朴素的“计数”,是数学的起点。
整数:有了“冷酷”的负数
然而,生活并不会一直阳光明媚,我们会遇到零下摄氏度或银行账户里显示的“负余额”:信用卡透支或房贷(提到这个话题,笔者心里总是沉甸甸滴~)。
为了描述这种现象,我们引入了 整数。整数不仅包括正数,还包括 负数,以及它们之间的平衡者——0。因此,整数的完整集合是:
ℤ = { …, -3, -2, -1, 0, 1, 2, 3, …}
整数不仅帮助描述正向的世界,也让我们理解“负面”的现象。
有理数:分配的艺术

当我们学会把一个苹果分给两个人时,有理数就应运而生了。
有理数是可以表示为两个整数之比(即分数)的数,形式如下: a/b,其中 a, b ∈ ℤ, b ≠ 0
(我们没法把苹果分给“0”个人,所以分母不能为零,不然数学家真的会抓狂)。
- 除以 0 没有意义:如果分母为 0,无法找到任何数乘以 0 得到非零的结果,这样就会导致数学上的矛盾。
有理数,比如 1/3, 355/106, -2/3,甚至整数本身也是有理数,因为它们总是可以写成 n/1 的形式。
有理数的作用无处不在,但凡涉及“分配”或者“比例”,它们就会闪亮登场。
实数:无理数的加入
有理数家族已经够庞大了,但你以为这就是全部了?不不不,欢迎来到更广阔的实数世界!实数不仅包括有理数,还包括那些无法用分数表示的“神奇数”——无理数。

无理数的名字听起来有点“无理取闹”。要知道,古希腊毕达哥拉斯学派坚信,所有的事物都可以用整数或整数之比来表达:世界应当是整洁、有理且可以度量的。
不过其中一位成员希帕索斯在研究边长为 1 的等腰直角三角形的斜边长度时,发现结果竟然是 √2。他尝试用整数或分数来表达这个结果,可失败了——它无法用两个整数的比来表示,它的小数部分是无限不循环的,比如 √2 = 1.414213562373095...

就这样一直延续下去,还永远找不到重复的规律。
常见的无理数还包括:π(圆周率)、e(自然对数的底数)、φ(黄金分割比)、√3 等。
因此,实数包括了所有的有理数和无理数,形象地说,实数就是数轴上所有的点,从左到右,无穷无尽。

代数数 vs. 超越数:谁更高深?
接下来,会遇到了两个稍微抽象的概念:代数数和超越数。
代数数是那些能够成为某个整数系数多项式方程解的数。比如,3x² - 9x + 6 = 0 的解是 x = 1 和 x = 2,因此它们两个是代数数。
代数数不仅包括有理数,还包括一些无理数。比如,√2 就是方程 x² - 2 = 0 的解,φ 是方程 x² - x - 1 = 0 的解,所以它们也都是代数数的一员。
但并不是所有的数都能被整数系数多项式方程“驯服”。有些数,无论你如何组合整数系数的多项式,它们都不会成为解。这些数被称为超越数。
最著名的例子就是 π 和 e。无论你怎么组合整系数的多项式,它们就是不愿意成为方程的解。
复数:虚数和实数的完美结合
你以为故事就到这里结束了?不,欢迎来到 复数的世界。复数是由一个实数部分和一个虚数部分组成的,形式为 a + b,其中 是虚数单位,也是方程 x² + 1 = 0 的解—— 也是一个代数数。

虚数听起来有点像魔法,但它们非常实用,特别是在物理学、电力学和工程中有广泛的应用。通过复数,人们可以处理那些仅用实数无法解决的问题。
数的世界远不止于此
数的世界远不止这些,还有许多更高级的数系等待探索。
比如,四元数和 八元数扩展了复数,帮助人们处理三维和更高维的旋转问题;p 进数则在数论中扮演着重要角色,它通过质数的视角重新定义了“距离”,并为数论中的整除性和同余问题提供了强有力的工具。还有 超复数,如 双曲数和 双数,它们在物理和工程中有着特殊的应用,尤其是在处理时空几何和自动微分问题时。如果你认为无穷小只是微积分中的抽象概念,那么 超实数将颠覆你的想法,它们让无穷小和无穷大的操作变得严格且可行。
每一种数系都是理解世界的钥匙。而你我,正站在这条通向无限的道路上,保持好奇心,勇敢追寻!
(责任编辑:综合)
-
 随着网络发展,个别网民通过网络平台故意发布虚假信息或评论,对社会秩序造成了不良影响。 记者从潮州市公安局获悉,近日,潮州市公安局巡查发现谢某、张某、苏某、蔡某、戴某等人先后在网上发布“被要求整改
...[详细]
随着网络发展,个别网民通过网络平台故意发布虚假信息或评论,对社会秩序造成了不良影响。 记者从潮州市公安局获悉,近日,潮州市公安局巡查发现谢某、张某、苏某、蔡某、戴某等人先后在网上发布“被要求整改
...[详细]
-
 朝鲜外务省10月11日发表重大声明,称韩国的反朝军事活动“正在越过危险界线”。声明称,韩国使用无人机向朝鲜首都平壤进行“政治军事挑衅”——韩国在10月3日、9日和10日使用无人机“侵入平壤上空,散
...[详细]
朝鲜外务省10月11日发表重大声明,称韩国的反朝军事活动“正在越过危险界线”。声明称,韩国使用无人机向朝鲜首都平壤进行“政治军事挑衅”——韩国在10月3日、9日和10日使用无人机“侵入平壤上空,散
...[详细]
-
 原标题:SpaceX:发射塔的机械臂成功夹住返回地面的超级重型火箭“Super Heavy”) 财联社10月13日电,SpaceX表示,发射塔的机械臂成功夹住了返
...[详细]
原标题:SpaceX:发射塔的机械臂成功夹住返回地面的超级重型火箭“Super Heavy”) 财联社10月13日电,SpaceX表示,发射塔的机械臂成功夹住了返
...[详细]
-
 10月11日,2024斯诺克武汉公开赛半决赛进行,中国小将斯佳辉同特鲁姆普交手。本场比赛斯佳辉手感火热,打出了个人生涯首杆满分杆,此外还有两杆破百,最终斯佳辉6-2将特鲁姆普淘汰出局,职业生涯首次战胜
...[详细]
10月11日,2024斯诺克武汉公开赛半决赛进行,中国小将斯佳辉同特鲁姆普交手。本场比赛斯佳辉手感火热,打出了个人生涯首杆满分杆,此外还有两杆破百,最终斯佳辉6-2将特鲁姆普淘汰出局,职业生涯首次战胜
...[详细]
-
 来源:都市时报 近日,浙江宁波不少网友在社交平台吐槽宁波地铁4号线车厢里的广告。 据网友拍摄图显示,地板上贴着一支穿着鲜艳旧时服饰迎亲的队伍的,有网友认为鲜艳的颜色与车厢不搭,有网友认为把人像
...[详细]
来源:都市时报 近日,浙江宁波不少网友在社交平台吐槽宁波地铁4号线车厢里的广告。 据网友拍摄图显示,地板上贴着一支穿着鲜艳旧时服饰迎亲的队伍的,有网友认为鲜艳的颜色与车厢不搭,有网友认为把人像
...[详细]
-
 △贾巴利亚难民营 总台记者获悉,以色列军方当地时间14日上午对加沙地带北部贾巴利亚难民营的一个食品分发中心发动炮击,造成至少10人死亡,另有40人受伤,其中大部分是老年人和妇女。总台记者 李超)点击
...[详细]
△贾巴利亚难民营 总台记者获悉,以色列军方当地时间14日上午对加沙地带北部贾巴利亚难民营的一个食品分发中心发动炮击,造成至少10人死亡,另有40人受伤,其中大部分是老年人和妇女。总台记者 李超)点击
...[详细]
-
 碘是合成甲状腺激素的必需物质,而甲状腺激素在调节新陈代谢、促进胎儿大脑发育等方面起着重要的作用。孕妇如果缺碘,不仅会影响自身的健康,更可能导致流产、死产、新生儿智力低下等问题。由于地理环境和饮食习惯的
...[详细]
碘是合成甲状腺激素的必需物质,而甲状腺激素在调节新陈代谢、促进胎儿大脑发育等方面起着重要的作用。孕妇如果缺碘,不仅会影响自身的健康,更可能导致流产、死产、新生儿智力低下等问题。由于地理环境和饮食习惯的
...[详细]
-
 [环球时报综合报道]鲑鱼子堆得高高的海鲜盖饭、现烤北海道和牛……这是位于北海道札幌市中心薄野商业区的一家商务酒店的早餐情况。目前日本物价高涨,酒店都抱怨“无利可图”,但早餐之争却不容有失。 据《
...[详细]
[环球时报综合报道]鲑鱼子堆得高高的海鲜盖饭、现烤北海道和牛……这是位于北海道札幌市中心薄野商业区的一家商务酒店的早餐情况。目前日本物价高涨,酒店都抱怨“无利可图”,但早餐之争却不容有失。 据《
...[详细]
-
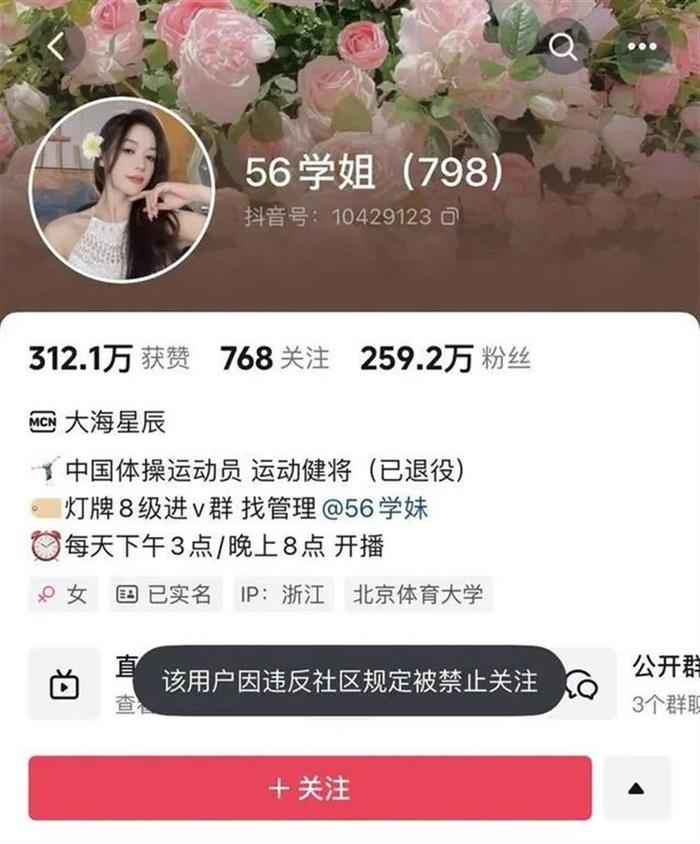 极目新闻评论员 石平 近日,退役体操运动员吴柳芳因投身网红主播,大跳性感舞蹈展示身材被指“擦边”引发热议,甚至体操奥运冠军管晨辰与她还发生了“口水仗”。11月24日晚,吴柳芳的短视频账号显示“因
...[详细]
极目新闻评论员 石平 近日,退役体操运动员吴柳芳因投身网红主播,大跳性感舞蹈展示身材被指“擦边”引发热议,甚至体操奥运冠军管晨辰与她还发生了“口水仗”。11月24日晚,吴柳芳的短视频账号显示“因
...[详细]
-
 据欧洲地中海地震中心报告,当地时间10月12日11时43分,哥斯达黎加发生6.2级地震,震源深度25公里。 目前暂无人员伤亡及财产损失报告。总台记者 马天静)
...[详细]
据欧洲地中海地震中心报告,当地时间10月12日11时43分,哥斯达黎加发生6.2级地震,震源深度25公里。 目前暂无人员伤亡及财产损失报告。总台记者 马天静)
...[详细]

 空中俯瞰长城全貌 慕田峪长城开通低空游览航线
空中俯瞰长城全貌 慕田峪长城开通低空游览航线 王楚钦无缘亚锦赛4强
王楚钦无缘亚锦赛4强 大美中轴线观光巴士吸引游客打卡
大美中轴线观光巴士吸引游客打卡 美乌佛州会谈结束 俄乌和平契机是否到来?专家分析
美乌佛州会谈结束 俄乌和平契机是否到来?专家分析
